[Part 1] (originally published December 10, 2012)
You’re appearing on the “hottest new game show” Money to Burn. You’ll be playing two rounds of a game theory classic against the host with a typical “Money to Burn” twist. If you can earn more than $100, you get to move on to the next round.
One of the current problems in (and arguably with) game theory is the so-called “centipede game” (Rosenthal 1981) – where the so-called logical/rational/correct/”optimal” strategy produces virtually the worst possible result. While there are many variants of the centipede game, they all take the form of players alternately choosing between increasing the pot and continuing the game –or– “cashing out” by taking the majority of the pot and ending the game. The “problem” posed by the game is that the current player has to choose between “selfishly” taking a sure thing or trusting the other player to be unselfish – in a game where a finite ending guarantees that one of the two will end up with less than they could have gotten if they’d just ended the game a turn earlier.
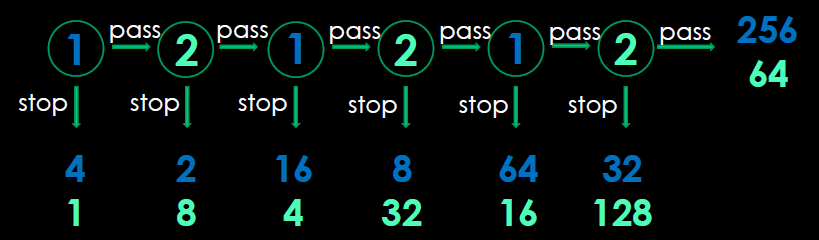
In the most common variant, the game starts with two piles of money lying on the table – one pile with four one-dollar bills and a second “pile” with a single one-dollar bill. The first player has two options, to stop or to pass. If he stops, the game ends and he gets the larger pile ($4) while the second player gets the remaining pile ($1). If he continues, the two piles are doubled to $8 and $2, and the second player is faced with a similar decision with twice the stakes: either to take the $8 pile, thus ending the game and leaving the $2 pile for the first player, or to let the piles double again and let the first player choose again. This continues for at most six choices. If neither of the players has stopped by then, the first player gets $256 and the second player gets $64. This is diagrammed below.
You are going to play this variant twice (once going second and once going first) against the game show host – who, in standard Money To Burn fashion, is going to literally burn any of the money that he wins. To make it a true logic puzzle (rather than a guessing game), you must first write down your strategy for both of the games and then the host is required to make the decisions that result in his burning the greatest amount of money (in much the same way that a blackjack dealer must “hit” on 16 or below and “stay” on 17 or above).
While this game offers both players a very profitable opportunity ($256/$64 or $32/$128), backward induction (one of the oldest ideas in game theory) predicts/dictates that the first player will/should stop at the first opportunity and win just $4. The reasoning behind this can be described as follows. On the last turn, player two has a choice between stopping and getting $128 and passing and getting only $64. “Obviously”, s/he will choose to stop. If this is true then, on the penultimate turn, player one really just has the choice between stopping for $64 or passing and getting only $32. Of course, this then means that, on the turn before, the second player just has the choice between $32 and $16 . . . and so on . . . until, on the first turn, the first player has a choice between $4 and $2 (and chooses $4).
The large discrepancy between the profits that intuition says are possible and what the “rationality” of backward induction dictated induced Rosenthal (in the very same paper in which he introduced the centipede game) to propose an alternative to the game theoretic approach in the hope of obtaining predictions more in line with intuition. And, indeed, one can certainly sympathize/agree with those individuals reported (Aumann 1992) to find the backward induction outcomes so disturbing that “if this is rationality, they want none of it” (pg. 218). So, it should come as no surprise that numerous subsequent papers were quickly able to demonstrate examples where violating backward induction is perfectly rational (due to the believed probability that the other player was unlikely to adhere strictly to the dictates of backward induction).
And, indeed, with the twist in the game show variant (that the game show host knows what your strategy is and *must* act to ensure that he burns the most money possible), a strategy of always passing will net you $32 + $64 = $96 (much higher – but still $4 short!). If you were player 1 first, you could make $256 + $64 = $320 with a strategy where you will only pass on your last choice as player 2 if the game show host passed on his last choice as player 2. But, of course, you start as player 2 and know that the host must break any promises that he makes which result in his burning less money.
But, what happens when players are perfectly rational and/or believe that the other player is likely to adhere strictly to the dictates of backward induction? Palacios-Huerta and Volij (2009) performed an experiment comparing when chess players played chess players, students played students, and chess players and students played each other. When chess players played chess players in one-shot games, 69% of the games ended with the first node. This percentage escalated to 100% when the first player was a Grand Master. Further, when chess players played ten repetitions, every game after the fourth repetition ended with the first node.
This is in marked contrast to the case of students playing students – where only 3% of the games ended at the initial node and there was no change to this behavior with repetition. Yet, in the treatments where students faced chess players as player 1, ten times as many of the games (30%) ended at the initial node and this percentage rose to 70% with repetition. And, when chess players faced students as the first player, they ended the games at the first node only 37.5% of the time (over 45% less than when they played other chess players). Thus, student players playing each other make the most money, followed by mixed competitions, with chess players playing each other making the least.
Aumann (1995) proves that it is “common knowledge of rationality” (rather than “rationality” itself) that causes the backward induction outcome to be reached. Yet, I would vigorously dispute that it is “rationality” which was the common knowledge since it causes the most “rational” to have the worst results (earn the least money). Indeed, it is at this point, I contend, that backward induction should have been relegated to the “correctness” category of “self-fulfilling prophecy” rather than the category of “game-theoretically *optimal*”. Yet, attempts to “prove” the “correctness” of backward induction through counter factual conditionals continue to be made by Aumann (1998) and the LessWrong “rationalists”.
Please don’t spoil the fun for others by posting successful solutions. If you wish to solve the puzzle by yourself, don’t read the next article in this series until you have done so or given up.
In the next article, I will reveal and explain the solution that allows advancement to the next round of Money to Burn. Then, I will show how that leads to a rational argument that will cause even the most ardent “rational” players to abandon the currently touted “optimal” strategy in favor of a newly proposed one. I will be touching upon whether it is true that the Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent and Does Unfairness Triumph After All? And, as usual, I’ll tie this all back to the current “existential risk/AGI enslavement” movement and what we should be doing instead.
Thanks go to Julie Waser for helping me “Make it so that a real person can understand the puzzle.”
[Part 2] (originally published December 23, 2012)
Contains three hints (one given previously) before the puzzle solution from Part 1 is revealed.
Before I lose my mathematical/logical audience, let me clearly state that backward induction is a logical operation that *always* functions correctly. Unfortunately, however, like so many similar operations, correct functioning upon garbage input most often includes outputting garbage (GIGO). This is clearly the case when using backward induction on the centipede game.
One of the standard assumptions in the centipede game is the following (from Part 1):
On the last turn, player two has a choice between stopping and getting $128 and passing and getting only $64. “Obviously”, s/he will choose to stop.
The puzzle from Part 1 was specifically designed to disprove this assumption. If this is your strategy when you are player two, the game show host will, by the rules, be forced to stop before you have this choice. If you make a similar choice when you are player one, you will never succeed in getting to the next round. Of course, if you choose to always pass, you won’t make enough money to get to the next round via that method either.
Hint 1: The optimal strategy does not guarantee that you get to the next round — but it *does* give you a greater than 95% chance of doing so.
The “trick” is to offer the “self-interested” game show host “an offer he can’t refuse”. If you were player one first, you could offer a strategy of always passing UNLESS the game show host stopped in the first game, in which case you stop immediately in game two. Given a choice between 128 + 4 = 132 if he stops and 64 + 256 = 320 if he passes, the game show host must always pass as well. But, alas, you are not going first (so as to prevent this strategy and the complaint that the two games are being tied together “inappropriately”).
Hint 2: The games should be considered separately and succeeding in stopping on your last turn in either game (both are possible) will move you on to the next round.
So how do you make it so that the game show host can’t prevent you from stopping?
According to the rules, the only way is to make it more worthwhile for him to let you reach that stopping point (remember his rules don’t care about how much you are making or whether you make it to the next round, they only care about how much money he gets to burn).
Hint 3: How do you “force” your opponent’s “optimal strategy” in a Nash Equilibrium?
WARNING! SOLUTION IMMEDIATELY FOLLOWS!
WARNING! SOLUTION IMMEDIATELY FOLLOWS!
WARNING! SOLUTION IMMEDIATELY FOLLOWS!
WARNING! SOLUTION IMMEDIATELY FOLLOWS!
WARNING! SOLUTION IMMEDIATELY FOLLOWS!
WARNING! SOLUTION IMMEDIATELY FOLLOWS!
The “trick” is to have your last turn strategies rely on the results of a future random event (like a coin-flip) that will give him an expected average outcome that is better than the outcome of his stopping before the event. For example, assume that your strategy is to pass on your first two turns of each game and then flip a coin on the last. In the first game, the game show host’s choices are to either stop at 64 or have a 50% chance of 32 and a 50% chance of 256 – for an expected average of (32 + 256) / 2 = 144. Given a choice between 64 and 144, he can’t refuse the offer of 144.
Similarly, in the second game, he has a choice between stopping at 32 or having a 50% chance of 16 and a 50% chance of 128 and must choose the average of 72 over 32.
With this strategy, only being unlucky with both coin-flips (50% x 50% = 25%) prevents you from moving onto the next round. But you can do *much* better. The equilibrium point, where the odds must be for the expected outcome to equal that of stopping, is actually at a probability of one-seventh. Any odds
better than one in seven, for example a die roll, will still force the game show host to allow the random event. Now only a roll of “snake-eyes” (1/6 x 1/6 = 1/36 < 95%) will prevent you from moving on.
Of course, with your typical luck, that is exactly what you roll – winning only $96 of the needed $100. Fortunately for you, that makes for bad television and you are moved on to the next round by the “statistical outlier” rule while the host cheerfully burns the maximum possible $384.
Backward induction is performed exactly like forward induction. First, you prove that a single case is true.
Then, you prove that if a given case it true, then the neighboring case is true. All cases of induction most often simply produce garbage if either of the two proofs is invalid.
The centipede game case errs by claiming to have proved the case of the last turn *in isolation* and then claiming that it is still solved identically in the context of a neighboring case. But, realistically, once the previous turn is considered, there never exists a case of 64 vs. 128 which is a slam-dunk *unless* either the previous player is willing to accept 32 rather than 64 – OR – s/he believes that there is some probability that the answer to 64 vs. 128 is not a foregone conclusion in favor of the 128. If neither is true, the previous player will stop and create the paradox of a choice which operates backwards in time to cause its own non-existence (like an evil AI black-mailing you from a possible future in order to ensure its creation).
Seeming paradoxes in logic *always* mean that either you don’t understand the problem or you’ve got faulty assumptions or both. The most egregious “sins of game theory” aren’t where game theory is incorrect but where results derived under (and depending upon) very specific circumstances are inappropriately generalized and expected to hold when critical assumptions are invalidated under the generalization. Another example of bad assumptions ruining backward induction is the so-called “hanged man paradox”.
An arrogant reductionist was brought before the king who believed all reductionists to be a danger to his realm. The reductionist knew that the king was good to his word and would not break it even if it meant releasing him so he quickly constructed a logical trap. After being informed that he was going to be hanged in the current month and asked his last wishes, reductionist claimed that he loved surprises and asked that the date of his execution be a surprise and that he not realize it until he was told at 7:00 AM on the day of his hanging – or that the king relent and pardon him at the end of the month.
The king, being a great deal wiser and having seen this all before, acted confused but agreeable. The reductionist immediately leapt on the chance and started “Well then, I can’t be executed on the last day of the month because then I would know the date and couldn’t be surprised.” The king pondered and pondered and eventually doubtfully said “It would certainly seem so.” So the reductionist continued “And I can’t be executed on the day before that because I know that I can’t be executed in the last day and therefore the next to last day is the only day possible, so I will know that it is then and won’t be surprised and can’t be executed. The king looked even more doubtful and said “Are you sure?” The reductionist excitedly claimed “Yes, absolutely” and went on to argue that he couldn’t be executed on any day of the month.
Now, the king really could have killed the reductionist at any time – since he would have been tremendously surprised to see his logic fail – but he had a lamentable fondness for baiting reductionists and wanted to make the most of the opportunity. He amused himself during the month by periodically showing up at 7:00 AM and seemingly allowing himself to be talked out of the execution as unsurprising – as the reductionist started looking forward to his reprieve and going home. And on the last day of the month, he sent the hangman in at 7:00 and the reductionist was executed after his last words of “But I knew that it had to be today so I couldn’t possibly be surprised and hanged.”
This series will continue with by discussing Rice’s theorem’s impact on reductionism and presenting a rational argument that should cause even the most ardent “rational” players to abandon the currently touted “optimal” strategy in favor of a newly proposed one. I will also be touching upon whether it is true that the Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent and Does Unfairness Triumph After All? And, as usual, I’ll tie this all back to the current “existential risk/AGI enslavement” movement and what we should be doing instead.
Finally, if you’re still looking for end-of-year charitable donations, I highly recommend both Transhumanity.net and the Digital Wisdom Institute.
References
Aumann R (1992) Irrationality in Game Theory. In Dasgupta P Gale D Hart O Maskin E (Eds) Economic Analysis of Markets and Games: Essays in Honor of Frank Hahn, 214-27. Cambridge: MIT Press.
Aumann RJ (1995) Backward Induction and Common Knowledge of Rationality. Games and Economic Behavior, 8(1): 6-19. http://www.elsevier.com/framework_aboutus/Nobel/Nobel2005/nobel2005pdfs/aum13.pdf
Aumann RJ (1998) On the Centipede Game. Games and Economic Behavior, 23(1): 97-105. http://www.ma.huji.ac.il/raumann/pdf/Centipede%20Game.pdf
Palacios-Huerta I Volij O (2009) Field Centipedes. American Economic Review 99(4):1619-1635. http://www.palacios-huerta.com/docs/Field%20Centipedes.pdf
Rosenthal RW (1981) Games of Perfect Information, Predatory Pricing and Chain Store Paradox. Journal of Economic Theory, 25(1): 92-100. http://www.professorchaing.com/files/Rosenthal_1981_JET.pdf

October 4, 2014 at 5:18 pm
comments from archive:
Very well written, very clear, and very interesting stuff. Thanks for this.
By Sam on Dec 27, 2012 at 5:48am
LessWrong rationalist do NOT support backwards induction in cases like these. In fact, they’re of much the same opinion as you: Rationalist should win, and if there is a better strategy to be used, then it is rational to do so.
By Tarn on Jan 04, 2013 at 7:59pm
|
|
By dsgghGranvilledsglds on Feb 02, 2013 at 12:14pm
Um, my strategy was:
In game 1, Pass, Pass, Stop.
In game 2, I will select (a) or (b): (a) if the host stopped in game 1, (b) if he didn’t. (a) is Stop, (b) is Pass, Pass, Pass.
So, in game 1, the host will pass straight through, and I collect $128. The host might think about stopping on his third turn, but if he does, he’ll only make $1 in game 2 to add to his $64 from game 1. If he doesn’t, he’ll take the maximum $256 from game 2 to add to his $32 from game 1.
This seems to be a better result than the one posed in the article. So, er, what did I misunderstand from the rules?
By Darren Reynolds on Dec 24, 2012 at 2:10am
[whoops – typo in the prevous post!]
Um, my strategy was:
In game 1, Pass, Pass, Stop.
In game 2, I will select (a) or (b): (a) if the host stopped in game 1, (b) if he didn’t. (a) is Stop, (b) is Pass, Pass, Pass.
So, in game 1, the host will pass straight through, and I collect $128. The host might think about stopping on his third turn, but if he does, he’ll only make $1 in game 2 to add to his $64 from game 1. If he doesn’t, he’ll take the maximum $128 from game 2 to add to his $32 from game 1.
This seems to be a better result than the one posed in the article. So, er, what did I misunderstand from the rules?
By Darren Reynolds on Dec 24, 2012 at 2:51am
Hi Darren!
You gain $128 from game one and $32 from game two for a total of $160.
The expected value of the posted solution is 5/6 * $256 + 1/6 * $32 + 5/6 * $128 + 1/6 * $64 = $336 (more than twice as much).
On the other hand, for the tremendously risk-averse, your solution DOES indeed guarantee passing through to the next round whereas the posted solution has a small (although obviously possible) chance of not passing you through (since the “statistical outlier” rule was not given in the problem).
So give yourself credit for finding a way to the next round that I missed!
By Mark Waser on Dec 26, 2012 at 8:40am
yay!
At the risk of being an arsehole, I am not able to find anything in the text posing the challenge that the objective is to win as much money as possible. Instead, there is this: “If you can earn more than $100, you get to move on to the next round.”
Whilst it is not stated what the next round involves, I took that as they key objective. Therefore, 100% chance is better than 95% chance.
grin
By Darren Reynolds on Dec 27, 2012 at 4:51am